Comparaison de langages de programmation (2)

Date: 2025-04-22

Tags: C soft stats

Dans l’article précédent, le langage Rust était nettement plus performant que le langage C alors qu’il est censé être une référence en termes de performances.

On va essayer d’exécuter des benchmarks pour voir ce qui est optimisable à partir du code précédent.

Code original

On va chercher à optimiser ce code original :

#include <stdio.h>
#include <stdlib.h>
#include <time.h>

int main(int argc, char **argv) {
    unsigned long n;
    double x, y;
    unsigned long count = 0;
    unsigned long i;
    srand((unsigned)time(NULL));

    if(argc < 1)
        return 1;
    if(argv[1] < 0)
        return 1;
    else
        n = atoi(argv[1]) * 1024;

    for(i=0; i<n; i++) {
        x = (double) rand() / RAND_MAX;
        y = (double) rand() / RAND_MAX;
        if(x*x+y*y < 1)
            count++;
    }
    printf("%f\n", (double) 4 * count / n);

    return 0;
}

Le code peut se décomposer :

1. Directives de compilation : influence négligeable sur la durée d’exécution
2. Déclaration de variables : adapter la taille des variables affecte l’utilisation de mémoire et peut affecter les opérations entre variables
3. Lecture et décodage de paramètres : opération relativement lente, mais exécutée une seule fois
4. Boucle : itérée n fois, devrait représenter la plus grande partie de la durée d’exécution du programme
   1. Génération d’un nombre aléatoire, cast et division
   2. Idem
   3. Deux multiplications, une somme et une comparaison entre des variables de type double
   4. Incrémentation d’un nombre entier
5. Affichage : opération très lente, mais exécutée une seule fois

Mesure des durées d’exécutions

On va utiliser la fonction clock_gettime()¹ de la bibliothèque time.h, qui a un compteur en nanosecondes avec une résolution inférieure à 100ns en fonction des systèmes. Il semblerait que la variable soit un entier signé de type long, soit 32 bits sur ma machine. Seulement les valeurs positives sont utilisées, ça veut dire que la variable déborde toutes les 2^31 ns, ce qui correspond à 2.14 s. Il va falloir être prudent et se limiter à des cas où l’exécution dure moins longtemps, et retirer les cas où la variable déborde.

On va donc écrire une fonction nanos() qui retourne la valeur de ce compteur :

#define _POSIX_C_SOURCE 199309L

struct timespec ts;

unsigned long nanos() {
    clock_gettime(CLOCK_MONOTONIC_RAW, &ts);
    // ignoring errors or overflows,
    // should be fine: 2^31 = 2.14s on this system,
    // possibly 2^63 ns = 9.2e9 s = 292 years on some systems
    return (unsigned long)ts.tv_nsec;
}

Cette fonction peut-être appelée avant et après chaque bloc de code marqué en gras dans la section précédente, pour mesurer la durée de son exécution. Il est important de ne pas l’appeller dans la boucle, vu que ça perturberait la mesure de la durée de son exécution.

Résultats de mesures

On passe le paramètre 1000 au programme, qui correspond à 1’024’000 itérations de boucle, et qui devrait s’exécuter en moins de 2.14 s.

On va mesurer les temps d’exécutions 100 fois pour supprimer manuellement les points aberrants.

Note : le langage Bash et ses outils associés sont idéaux pour ce genre d’opérations :

for i in $(seq 0 100); do montecarlo_pi_opt 1000; done | awk 'NR%2 == 0' > benchmark/c_timings

On utilise ensuite GNUplot pour calculer les statistiques.

Bloc	Durée d’exécution [us]	Std dev
Décodage de paramètres	5.6	1.7
Boucle	37.99e3	639
Affichage	43.3	9.4

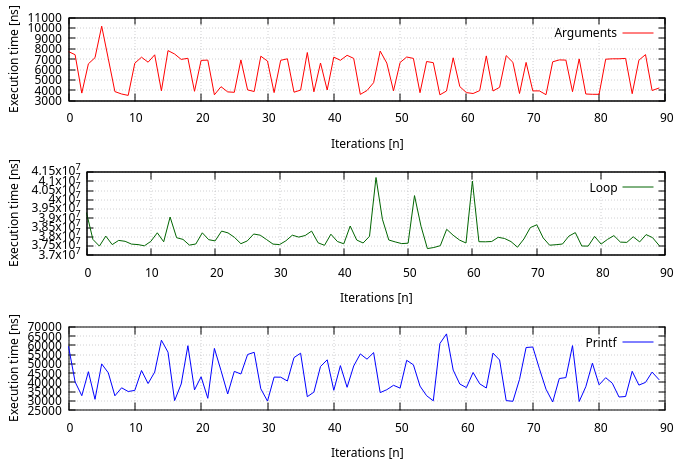
Les mesures confirment les suppositions : améliorer le décodage de paramètres et l’affichage auraient des gains négligeables. Il faut donc se concentrer sur la boucle.

En moyenne, chaque itération de boucle devrait s’exécuter en 37.1 ns, on va voir ce que l’on peut gagner.

Optimisations du code de la boucle

Test

On va remplacer le code suivant :

if(x*x+y*y < 1)
    count++;

Par celui-ci :

count += (x*x+y*y < 1);

On remplace une opération logique par un cast de Bool vers long int, ce qui peut avoir une influence.

Variables

On avait choisi des variables entières de types unsigned long par défaut, alors que des variables de type unsigned int suffisent pour tous les nombres entiers manipulés, en considérant n = 102’400’000 itérations de boucles dans l’article précédent.

Division

Les divisions sont réputées pour être lentes, alors on va calculer un facteur hors de la boucle et le remplacer par des multiplications.

Ce code est remplacé :

for(i=0; i<n; i++) {
    x = (double) rand() / RAND_MAX;
    y = (double) rand() / RAND_MAX;

Par le code suivant :

const double normalize = 1 / RAND_MAX;

for(i=0; i<n; i++) {
    x = (double) rand() * normalize;
    y = (double) rand() * normalize;

Division2

On peut tenter de passer d’un nombre de type int à un nombre de type double avec des opérations bit-à-bit en séparant la partie fractionnaire de l’exposant².

On remplace ce code existant :

x = (double) rand() / RAND_MAX;
y = (double) rand() / RAND_MAX;

Par celui-ci :

random = rand();
x = (random & 0x1FFFFFFFFFFFFF) | (random & 0x3FF) <<53;
random = rand();
y = (random & 0x1FFFFFFFFFFFFF) | (random & 0x3FF) <<53;
// fraction part: 9007199254740991 (2^53) + exponent part

Ce type d’astuces peut rappeller le célèbre bricolage $\frac{1}{\sqrt{x}}$ utilisé dans Quake 3³.

Rand

La génération de nombre aléatoire est lente, on va mesurer la vitesse de ses appels en remplaçant ce code :

for(i=0; i<n; i++) {
    x = (double) rand() / RAND_MAX;
    y = (double) rand() / RAND_MAX;

Par ce code :

int a, b;

for(i=0; i<n; i++) {
    a = rand();
    b = rand();

Ce code ne doit pas fonctionner, mais simplement tester les performances de la fonction rand().

All

On va aussi effectuer toutes les modifications qui améliorent la vitesse d’exécution du programme et qui fonctionnent correctement.

Résultats

Optimisation	Durée d’exécution [us]	Std dev
Original	38.6e3	1.28e3
Test	38.5e3	1.11e3
Variables	38.5e3	1.45e3
Division	38.0e3	1.10e3
Div2	76.4e3	2.44e3
Rand	37.3e3	0.90e3
All	38.4e3	1.05e3

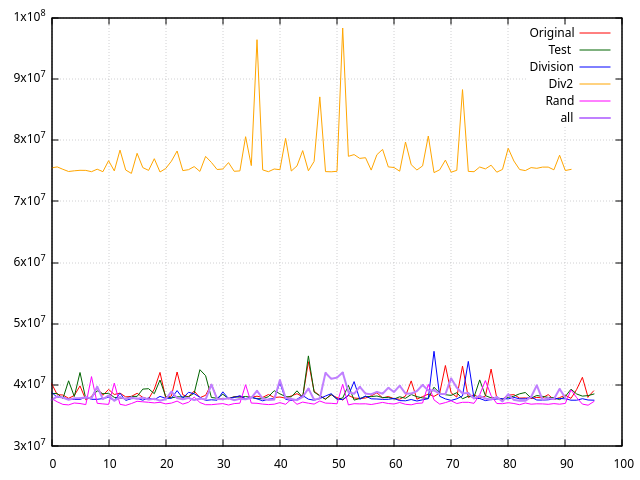
On peut voir que notre tentative de division de double est moins optimisée que la division du compilateur. Le seul cas qui est systématiquement plus rapide est celui où on ne met pas les nombres aléatoires en forme.

Les autres optimisations permettent de légères améliorations qui restent inclues dans l’écart-type, et ne sont pas significatives.

Réécriture du code

La gestion des nombres entiers est connue pour être plus rapide que celle des nombres à virgule flottante, et on a pu voir qu’il suffisait de ne pas calculer de division dans la boucle pour gagner en performances. On va donc réecrire le code en utilisant des nombres entiers dans la boucle, et en n’utilisant qu’un seul calcul à virgule flottante à la fin.

int main(int argc, char **argv) {
    unsigned long n;
    unsigned long x, y;
    unsigned int count = 0;
    unsigned int i;
    srand((unsigned)time(NULL));

    if(argc < 1)
        return 1;
    if(argv[1] < 0)
        return 1;
    else
        n = atoi(argv[1]) * 1024;

    for(i=0; i<n; i++) {
        x = rand();
        y = rand();
        count += (x*x+y*y < (unsigned long)RAND_MAX*RAND_MAX);
    }
    printf("%f\n", (double) 4 * count / n);

    return 0;
}

Résultats

On peut utiliser hyperfine avec les mêmes paramètres que dans l’article précédent : une itération de warmup pour précharger les fichiers en cache, et 15 itérations de mesure.

File	Mean [s]	Relative
Original	3.836 ± 0.026	1.02 ± 0.01
Integer	3.747 ± 0.018	1.00

La durée d’exécution se rapproche de celle des tests précédents où on évitait les divisions dans la boucle.

Optimisations du compilateur

Le compilateur GCC permet généralement des optimisations, qui sont souvent des compromis entre la compatibilité, la taille du fichier exécutable et les performances⁴.

Les célèbres CFLAGS -fomit-frame-pointer, -ffast-math et -funroll-loops sont généralement inclus avec -Ofast quand ils ne sont pas contre-productifs ⁵. -Os n’est pas censé augmenter les performances, mais les optimisations de taille mémoire peuvent aussi augmenter les performances par effet de bord. Cette optimisation a longtemps été recommandée de façon non-officielle avec la distribution de Linux Gentoo⁶.

Comme on va mesurer la durée d’exécution du programme complet et qu’une durée plus longue est moins sensible aux erreurs de mesure, on va augmenter le nombre d’itérations à : n = 1024’000’000.

CFLAGS	Mean [s]	Relative
O0	38.888 ± 0.273	1.05 ± 0.01
O2	37.696 ± 0.224	1.02 ± 0.01
O3	37.701 ± 0.248	1.02 ± 0.01
Os	37.157 ± 0.059	1.00 ± 0.00
Ofast	37.066 ± 0.022	1.00
Ofast_march	37.074 ± 0.025	1.00 ± 0.00
O2_march	37.441 ± 0.054	1.01 ± 0.00

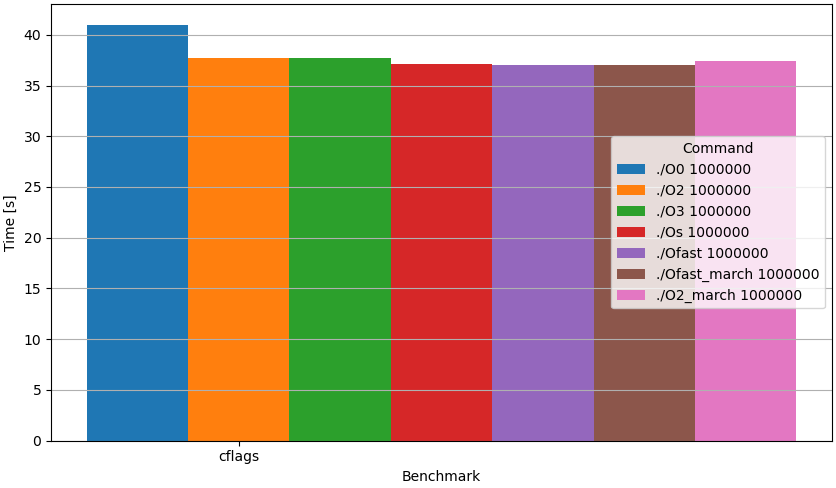
La commande strip⁷ est connue pour supprimer les symboles de debug, ce qui rend les fichiers exécutables plus compacts. L’amélioration des performances est surtout liée aux accès disques et éventuellement au début de l’exécution du fichier. Ça ne montre aucune différence mesurable.

Résultats

Tous ces tests montrent des gains en vitesse d’exécution de l’ordre de 5%. Les subtilités d’écriture ont une influence négligeable, alors que les stratégies d’algorithme et les options de compilateur ont une influence modérée.

Tous ces tests montrent que le paramètre limitant est bien le générateur de nombres aléatoires.

Là aussi, le code source est disponible⁸ sous license CC BY-NC.

Références

---

1. clock_gettime(3) - Manpage↩︎

2. Double-precision floating-point format - Wikipedia↩︎

3. Fast inverse square root - Wikipedia↩︎

4. Safe CFLAGS - Gentoo wiki↩︎

5. Optimize Options - GCC↩︎

6. CFLAGS -O3 vs. -Os - Gentoo Forums↩︎

7. strip(1) - Manpage↩︎

8. Code source CC BY-NC.↩︎

• ← Previous page
  Comparaison de langages de programmation
• Next page →
  cms

Electronics Électronique puissance semiconducteur semiconductors power Hardware CPE INSA Xavier Bourgeois

Xavier