Comparaison de langages de programmation (3) : Autres langages

Date: 2025-05-10

Tags: soft benchmark

Articles

Cet article fait partie d’une série de plusieurs articles comparant les langages de programmation :

• Comparaison de langages de programmation : Méthode Monte-Carlo
• Comparaison de langages de programmation (2) : Optimisations en langage C
• Comparaison de langages de programmation (3) : Méthode Monte-Carlo avec d’autres langages
• Comparaison de langages de programmation (4) : Génération d’images
• Comparaison de langages de programmation (5) : Surface d’un disque

Quelques personnes m’ont recommandé d’autres langages de programmation, ou se sont proposées de tester d’autres solutions.

Dart

Grégoire¹ m’a proposé de tester le langage Dart², en compilant un fichier exécutable pour que je puisse le tester sur ma machine.

Listes

Il a utilisé une approche vectorielle, similaire à celle de Numpy avec Python :

void calculatePiUsingList(int n) {
    final random = Random();

    final count = List.generate(n, (_) {
        final x = random.nextDouble();
        final y = random.nextDouble();
        return x * x + y * y < 1 ? 1 : 0;
    }).reduce((value, element) => value + element);

    final piEstimate = 4.0 * count / n;
}

Le calcul est plus rapide qu’avec Numpy :

Time (mean ± σ): 5.257 s ± 0.093 s

Range (min … max): 5.189 s … 5.470 s 10 runs

Par contre, ça semble utiliser beaucoup de ressources système, on va regarder :

pmap -d $(ps ax |grep pi_dart |grep -v grep |awk '{print $1}') |awk '{ print $2}' |tail -n 1

945704K

Presque 1 GB. C’est beaucoup, mais moins que Numpy qui utilise 3.8 GB dans les mêmes conditions.

Boucles

Il a aussi utilisé un calcul par boucles, similaire au code C :

void calculatePiUsingLoop(int n) {

    final random = Random();
    var count = 0;

    for (var i = 0; i < n; i++) {
        final x = random.nextDouble();
        final y = random.nextDouble();
        if (x * x + y * y < 1) count++;
    }

    final piEstimate = 4.0 * count / n;
}

La durée d’exécution est légèrement plus courte qu’en langage C.

Time (mean ± σ): 3.155 s ± 0.039 s

Range (min … max): 3.130 s … 3.262 s 10 runs

Il est possible que ce cas soit similaire à la comparaison entre les langages C et Rust, où on teste plus les performances du générateur de nombres aléatoires que celles du langage en lui-même.

Multithread

Après avoir discuté de l’hypothèse selon laquelle le framework Dart serait capable d’utiliser plusieurs threads, Grégoire a proposé de coder une version multithread de son code :

Future<int> calculatePiInIsolate(int n) async {
    final receivePort = ReceivePort();
    await Isolate.spawn(_calculatePiPartial, [receivePort.sendPort, n]);
    return await receivePort.first;
}

void _calculatePiPartial(List<dynamic> args) {
    final SendPort sendPort = args[0];
    final int n = args[1];
    final random = Random();
    int count = 0;

    for (var i = 0; i < n; i++) {
        final x = random.nextDouble();
        final y = random.nextDouble();
        count += x * x + y * y < 1 ? 1 : 0;
    }

    Isolate.exit(sendPort, count);
}

Future<void> calculatePiUsingIsolates(int n, int numIsolates) async {

    final isolateSize = n ~/ numIsolates;
    final futures = <Future<int>>[];

    for (var i = 0; i < numIsolates; i++) {
        final size = (i == numIsolates - 1) ? n - isolateSize * i : isolateSize;
        futures.add(calculatePiInIsolate(size));
    }

    final results = await Future.wait(futures);
    final count = results.reduce((value, element) => value + element);

    final piEstimate = 4.0 * count / n;
}

Le calcul a lieu dans la fonction _calculatePiPartial(), et les autres fonctions servent à séparer des intervalles d’itérations et sommer des résultats partiels, et à permettre aux processus de communiquer.

Avec un CPU 2C/4T, isoler le programme en 2 divise la durée d’exécution par 2. Passer de 3 à 4 diminue légèrement la durée d’exécution, et augmenter le nombre d’isolations au delà de 4 augmente la durée d’exécution.

On choisit de séparer le programme en 4 :

Time (mean ± σ): 1.378 s ± 0.012 s

Range (min … max): 1.363 s … 1.396 s 10 runs

C++

Thibault me propose de tester la même chose en C++ :

#include <iostream>
#include <random>
#include <cstdlib>

int main() {
    int n = 1024*100000;
    int count = 0;
    std::random_device rd;
    std::minstd_rand gen(rd());
    for (int i = 0; i < n; i++) {
        double x = gen() / static_cast<double>(gen.max());
        double y = gen() / static_cast<double>(gen.max());
        if (x * x + y * y < 1.0) {
            count++;
        }
    }

    double pi_estimate = 4.0 * count / n;
    std::cout << pi_estimate << '\n';

    return 0;
}

Là aussi, c’est un peu plus rapide qu’avec le langage C :

Time (mean ± σ): 3.211 s ± 0.038 s

Range (min … max): 3.175 s … 3.304 s 10 runs

En cherchant un peu, on essaye de changer de générateur de nombres aléatoires en remplaçant la classe minstd_rand par mt19937 qui utilise un autre algorithme³ :

Time (mean ± σ): 4.816 s ± 0.026 s

Range (min … max): 4.774 s … 4.850 s 10 runs

Tant qu’à faire, on va essayer minstd_rand0, qui est un autre RNG :

Time (mean ± σ): 12.467 s ± 0.048 s

Range (min … max): 12.422 s … 12.582 s 10 runs

Raté, c’est plus lent, sauf que ça montre que les durées d’exécutions dépendent plus du RNG que du langage et de ses optimisations.

OpenMP

On revient au RNG original, mais on rajoute une astuce que Thibault voulait montrer : un programme multithread, qui devrait-être 2 à 4 fois plus rapide avec ma machine qui a un CPU 2 cores et 4 threads.

Le code est déjà plus complexe :

#include <iostream>
#include <random>
#include <vector>
#include <omp.h>

int main() {
    int n = 1024*100000;
    int count = 0;

    #if defined(_OPENMP)
    int num_threads = omp_get_max_threads();
    #else
    int num_threads = 1;
    #endif

    std::cout << "Nombre de threads : " << num_threads << std::endl;

    std::vector<int> local_counts(num_threads, 0);

    #pragma omp parallel
    {
        #if defined(_OPENMP)
        int thread_id = omp_get_thread_num();
        #else
        int thread_id = 0;
        #endif
        std::random_device rd;
        std::minstd_rand gen(rd());

        int local_count = 0;

        #pragma omp for
        for (int i = 0; i < n; i++) {
            double x = gen() / static_cast<double>(gen.max());
            double y = gen() / static_cast<double>(gen.max());
            if (x * x + y * y < 1.0) {
                local_count++;
            }
        }
        local_counts[thread_id] = local_count;
    }

    for (int i = 0; i < num_threads; ++i) {
        count += local_counts[i];
    }

    double pi_estimate = 4.0 * count / n;
    std::cout << pi_estimate << std::endl;

    return 0;
}

On commence par l’exécuter en single-thread :

Benchmark 1: ./montecarlo_pi_openmp_st

Time (mean ± σ): 3.288 s ± 0.076 s

Range (min … max): 3.238 s … 3.468 s

C’est légèrement plus lent que le code original en C++ utilisant le même RNG, sans-doute à cause des instructions utilisées par OpenMP.

Essayons avec tous les threads disponibles sur la machine, en rajoutant le CFLAG -fopenmp à la compilation :

Benchmark 2: ./montecarlo_pi_openmp

Time (mean ± σ): 1.283 s ± 0.126 s

Range (min … max): 1.190 s … 1.609 s

La durée d’exécution correspond bien aux résultats attendus :

./montecarlo_pi_openmp’ ran 2.56 ± 0.26 times faster than ‘./montecarlo_pi_openmp_st’

Java

Cette fois-ci, Thibault propose de tester le langage Java⁴ :

import java.util.Random;

public class EstimationPi {
    public static void main(String[] args) {
        int n = 1024*100_000;
        int count = 0;
        Random random = new Random();

        for (int i = 0; i < n; i++) {
            double x = random.nextDouble();
            double y = random.nextDouble();
            if (x * x + y * y < 1.0) {
                count++;
            }
        }
        double piEstimate = 4.0 * count / n;
        System.out.println(piEstimate);
    }
}

Curieusement, le langage Java est réputé lent et lourd, mais cet algorithme n’a pas besoin de créer/libérer des zones mémoires, qui sont des opérations réputées lentes avec Java :

Time (mean ± σ): 5.634 s ± 0.174 s

Range (min … max): 5.483 s … 6.012 s 10 runs

Comme indiqué par Thibault, la classe Random⁵ utilise le même algorithme de génération de nombres aléatoires que celui de stdlib testé avec le langage C.

L’implémentation de Java semble légèrement plus lente que celle du C.

Résultats

Langage	Dart loops	Dart lists	Dart MT	C++	C++ OpenMP	Java
Durée de compilation [ms]	?	?	?	710	750	-
Durée d’exécution [s]	3.16	5.19	1.38	3.21	1.28	5.63
Nombre de lignes	64	63	83	21	41	17
Profondeur de boucles	1	0	2	2	1

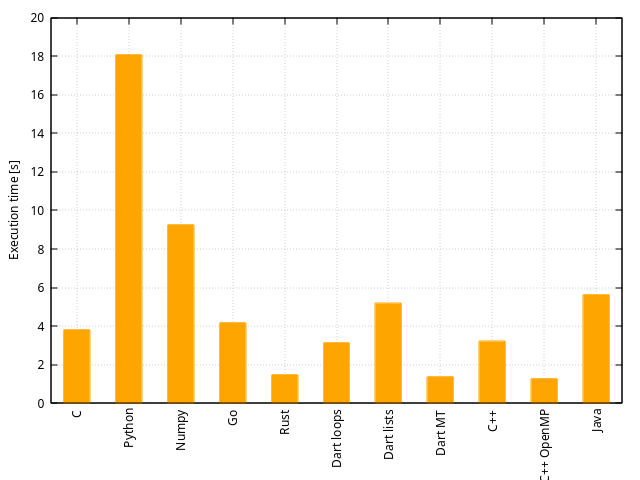
Cet algorithme est incorrect pour comparer les performances de langages de programmation puisqu’il dépend des performances du générateur de nombres aléatoires plutôt que celui du langage et de la compilation.

D’autres explorations sont nécessaires et seront développées dans des articles suivants.

Le code source est disponible⁶ sous licenses libres.

Références

---

1. Grégoire↩︎

2. Dart - Wikipedia↩︎

3. Mersenne Twister - Wikipedia↩︎

4. Java - Wikipedia↩︎

5. Random - Docs Oracle↩︎

6. Code source↩︎

• ← Previous page
  Comparaison de langages de programmation (2)
• Next page →
  Comparaison de langages de programmation (4) : Génération d'images

Electronics Électronique puissance semiconducteur semiconductors power Hardware CPE INSA Xavier Bourgeois

Xavier