Comparaison de langages de programmation (5) : Surface d'un disque
Date: 2025-05-20
Tags: C rust python soft benchmark pi
Articles
Cet article fait partie d’une série de plusieurs articles comparant les langages de programmation :
- Comparaison de langages de programmation : Méthode Monte-Carlo
- Comparaison de langages de programmation (2) : Optimisations en langage C
- Comparaison de langages de programmation (3) : Méthode Monte-Carlo avec d’autres langages
- Comparaison de langages de programmation (4) : Génération d’images
- Comparaison de langages de programmation (5) : Surface d’un disque
Les articles précédents montraient des incohérences entre les générateurs de nombres aléatoires, alors on va changer d’algorithme pour s’en passer. On va aussi éviter d’écrire dans des fichiers, limiter le nombre de divisions et l’utilisation de nombres à virgule flottante, pour ne pas trop désavantager certains langages.
Comme dans les cas précédents, le programme doit recevoir le nombre d’itérations depuis la ligne de commande, et afficher le résultat dans la console.
Et cette fois-ci, on va se permettre d’optimiser le code et la compilation dans les cas où c’est possible.
On mesure toujours les durées d’exécution avec Hyperfine1 avec une moyenne de 5 exécutions (10 à 100 en cas de jitter), mais on va donner une limite de durée arbitraire à 10 minutes par exécution. On va ensuite afficher graphiquement ces durées d’exécution, en faisant attention à ce qu’elles soient à la même échelle, pour permettre de comparer.
Approximation de Pi par calcul
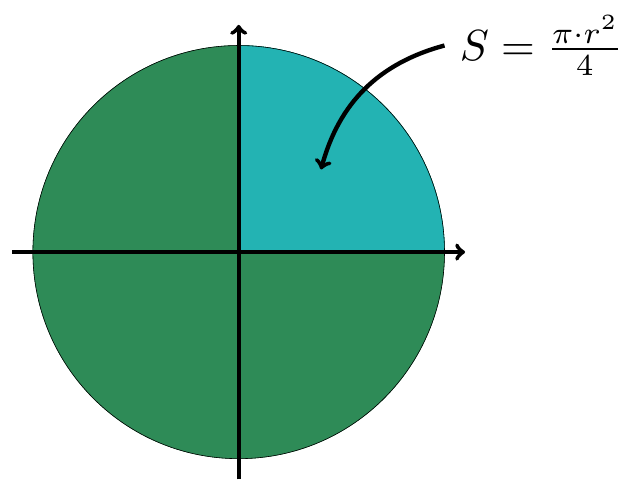
On considère un disque de rayon n, la surface de ce disque est donnée par . On a ainsi , et il reste ensuite à déterminer la surface de ce disque en balayant un rectangle de côté .
Dans ce cas, est arbitrairement limité à des valeurs entières. C’est encore une approximation, puisque est irrationnel et ne peut qu’être approché par une fraction. Cette approche peut-être considérée acceptable parce que les ordinateurs représentent des nombres à virgule flottantes2 comme une somme finie de nombres fractionnaires. Good enough.
Comme il s’agit d’un algorithme de complexité , il est intéressant de comparer les durées d’exécution pour plusieurs nombres d’itérations.
Algorithme pseudo-code
Load libraries
function integer compute_pi(integer n) {
declare integer count
declare integers i, j
count = 0
for(i in range(min=-n, max=n, step=1)) {
for(j in range(min=-n, max=n, step=1)) {
if(i*i + j*j <= n*n) {
count++
}
}
}
return result
}
main(cli_parameters) {
declare integer n, result
n = process(cli_parameters)
result = compute_pi(n)
print("pi = " + float64(result)/n*n)
}On choisit de calculer pi dans une fonction, pour permettre des optimisations par la suite.
Certains langages vont imposer des choix dès le début, comme la taille des nombres entiers qui peut causer des risques de débordements si elle est trop petite, ou être inutilement lente si elle est trop grande.3
Langage C
Écrire du code C est assez lent, où il faut réfléchir à l’exécution et parfois compiler le code pour vérifier le comportement.
Les types de variables sont explicites, mais on peut gagner en performances en écrivant deux fonctions différentes si on veut utiliser deux types de variables différents.
C’est ce qu’on va faire ici, avec des variables de types int de 32 bits et long int de 64 bits4. Le programme traite les paramètres de la ligne de commande, et appelle une fonction différente en fonction du nombre d’itérations5.
if(argc < 1) // checks if there is at least one CLI argument
return 1;
n = (int) abs(atoi(argv[1])); // reads 1st argument as n
if(2*n*n > INT_MAX) { // use 64 bit ints to avoid overflows, triggers at 32767
count = compute_int64(n);
}
else
count = compute_int32((int) n); // use faster 32 bit intsPerformances
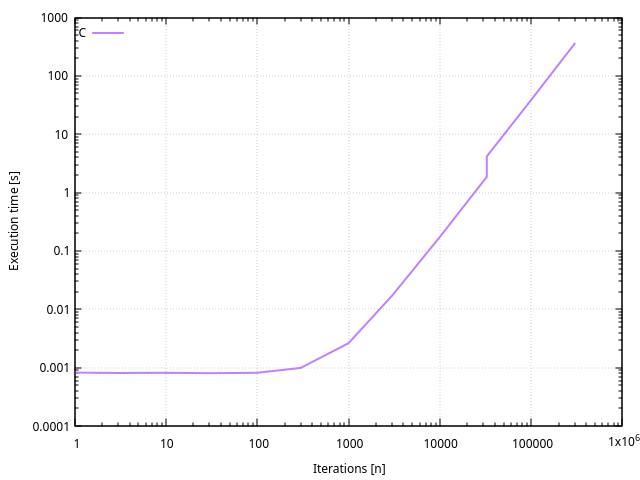
On peut y remarquer plusieurs choses intéressantes :
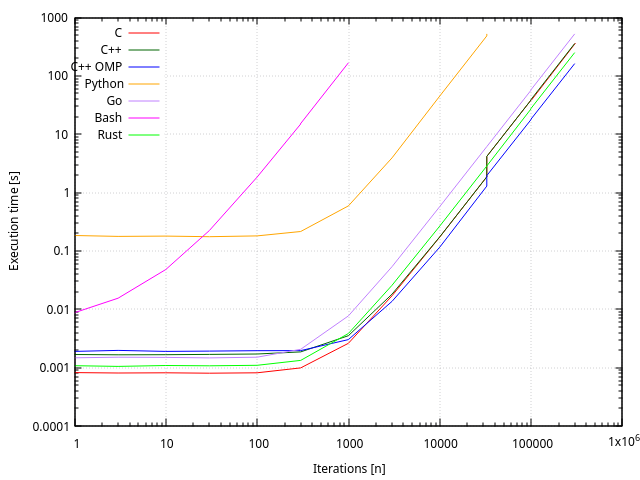
- L’allure générale de la courbe est une droite, avec deux axes en échelle logarithmique, ce qui correspond à une parabole en échelle linéaire. On a bien un algorithme de complexité O(n²).
- Les durées d’exécution inférieures à 5 ms sont difficiles à mesurer et à comparer6. La durée d’exécution des boucles devient négligeable devant la durée de chargement et de traitement du reste du programme.
- On remarque aussi un glitch au passage des entiers de 32 à 64 bits, entre les nombres d’itérations 32’767 et 32’768. La durée passe de 1.87 s à 4.17 s.
C++
Adapter le code C au langage C++ est direct et ne prend que quelques minutes. Cet algorithme n’utilise pas de spécificités de langages orientés objets, à l’exception des types automatiques du standard C++1178. On peut n’écrire qu’une seule fonction de calcul de pi, et l’appeller avec des paramètres de types différents :
if(argc < 1) // checks if there is at least one CLI argument
return 1;
long n = abs(atoi(argv[1])); // reads 1st argument as n
if(2*n*n < INT_MAX) // use 64 bit ints to avoid overflows, triggers at 32767
count = compute_int((int)n); // forces type
else
count = compute_int((long)n);Le code est simplifié, puisque c’est le compilateur qui va dupliquer la fonction compute_int(), dont le type des variables n, i et j est automatiquement choisi en fonction de leur valeur d’initialisation :
unsigned long compute_int(auto n) {
unsigned long count = 0;
auto i = -n;
auto j = -n;
for(i = -n; i <= n; i++) {
for(j = -n; j <= n; j++) {
if(i*i + j*j < n*n) {
count++;
}
}
}
return count;
}Performances
Il n’y a aucune surprise, l’exécution est identique à celle d’un programme en C avec les mêmes optimisations.
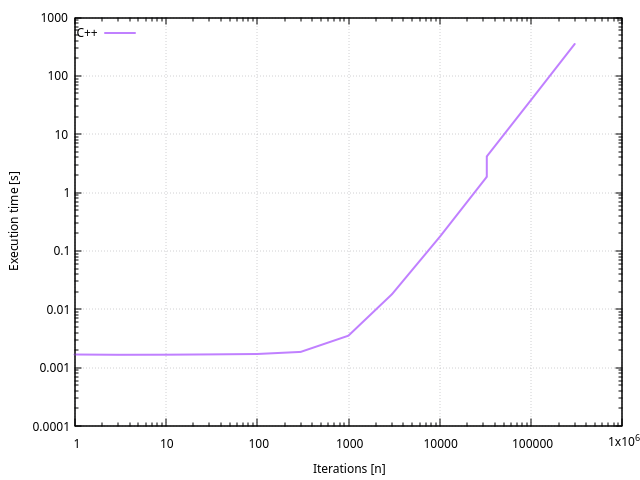
C++ OpenMP
Tant qu’à faire, on va utiliser la bibliothèque OpenMP conseillée par Thibault. Le code est identique au code C++ en y rajoutant les instructions liées à OpenMP9.
Performances
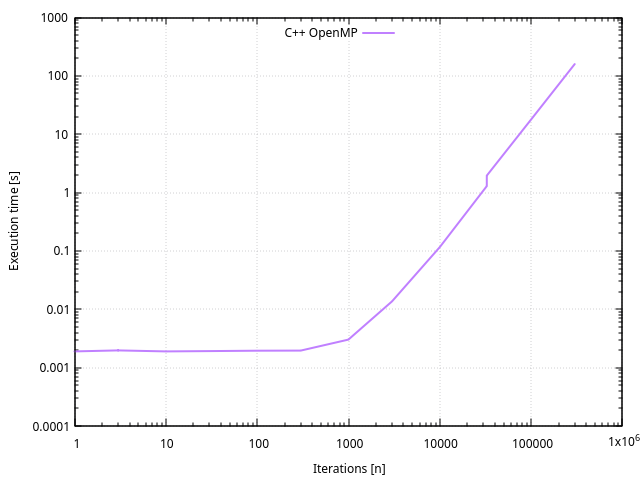
Comme on a un CPU à deux coeurs et 4 threads, la vitesse d’exécution est un peu plus que doublée.
Python
Python est exactement le contraire du langage C, où les types de variables sont implicites et le code se résume à une traduction directe de l’algorithme10.
Cet algorithme est constitué de boucles qui se vectorisent difficilement, Numpy impose d’utiliser une grande quantité de mémoire ( éléments de 1 à 4 octets), sans garantir que le traitement soit plus rapide que de parcourir deux boucles.
Performances
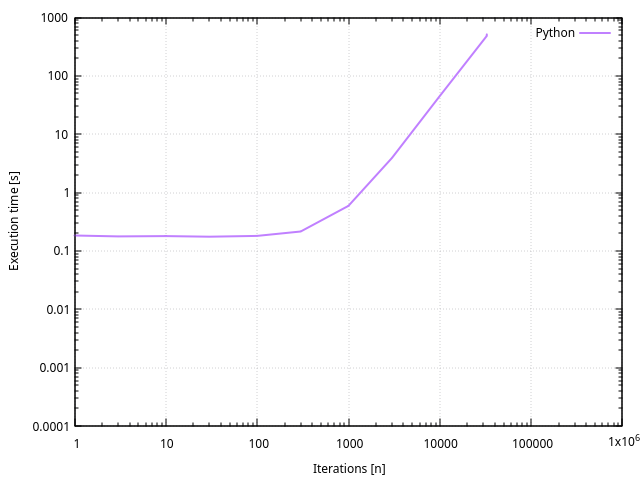
On peut remarquer que la durée d’exécution est quasiment constante pour des nombres d’itérations inférieurs à 300, et nécessite environ 300 ms, contrairement à moins de 10ms pour les langages compilés. Cette durée sert probablement à l’interpréteur Python qui analyse la syntaxe du code, pour le remettre en forme et l’exécuter.
Python s’exécute beaucoup plus lentement que le langage C, mais est plus rapide et efficace à coder.
Go
L’écriture du code Go est similaire à celle du code C sans aucune optimisation11.
Il faut remarquer que toutes les bibliothèques sont compilées de façon statique, ce qui peut entraîner de gros fichiers exécutables. Dans ce cas, le fichier a une taille de 1’804 kB, et la commande strip permet de ramener sa taille à 1’208 kB après suppression des symboles de debug.
Performances
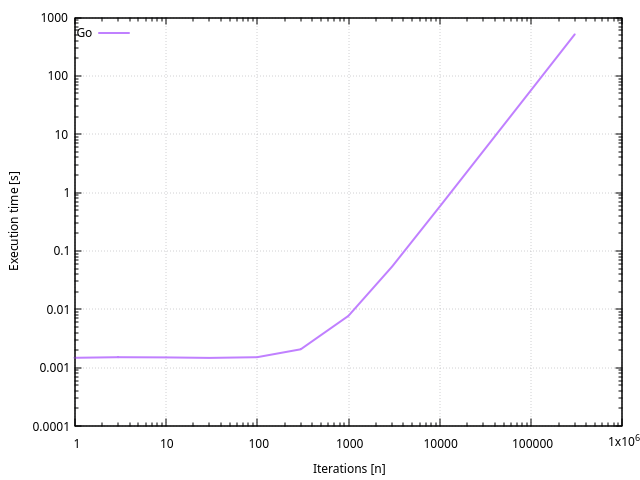
Le type int par défaut semble-être int6412. On n’observe pas de débordement et la durée d’exécution est proportionnelle à n².
Bash
Bash utilise des variables de type entières signées, mais leur longueur est implicite. On va essayer de la déterminer par expérience :
for i in 31 32 63 64 ; do echo $(( 2**$i -1 )); done2147483647
4294967295
4611686018427387903
9223372036854775807
-1
Ici, plus rien ne semble fonctionner au delà de 2^63, et le premier bit devrait être un bit de signe, que l’on peut vérifier en voyant la variable déborder :
echo $(( 2**63 ))-9223372036854775808
Bingo, Bash utilise bien des variables entières signées de 64 bits, et devrait se comporter comme les autres langages.
Comme Bash ne fonctionne qu’avec des nombres entiers, il faut appeller awk pour effectuer la dernière opération de division, avec des nombres de type double13.
#pi=$(awk "BEGIN { print $count / ($n * $n) }") # made prettier below
pi=$(awk "BEGIN { printf \"%g\t%.16g\t%.16g\n\", $n, $count / ($n * $n), 3.14159265358979323846 - $count / ($n * $n) }") # using M_PI from <math.h>
echo $piPerformances
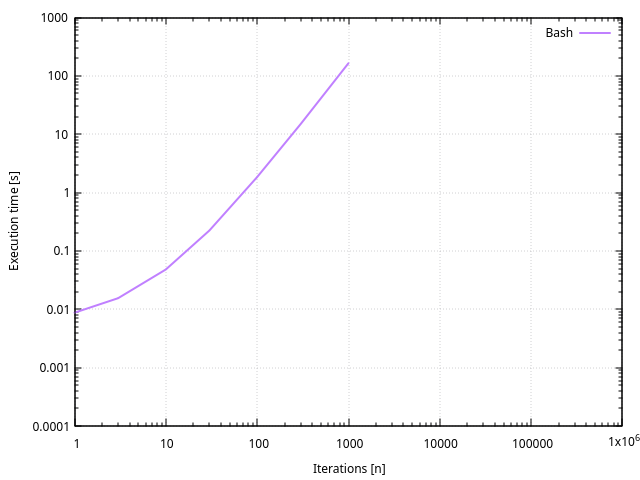
Si Python était lent par rapport au langage C, Bash est beaucoup plus lent que Python.
Rust
Avant d’essayer les mêmes astuces qu’en C, j’ai commencé par changer le type de variables, entre i32 et i64.
Sauf que l’exécution du programme est environ 50% plus lente avec des variables de type i32 que i64.
Le fichier exécutable a une taille de 11’376 kB, ça parait beaucoup trop gros en comparaison avec les résultats d’autres compilateurs. La commande strip permet de supprimer les symboles de debug et ramène la taille du fichier à 364 kB. C’est toujours 15 fois plus gros qu’un fichier exécutable codé en C, mais acceptable avec des bibliothèques inclues statiquement, comme avec le langage Go.
Performances
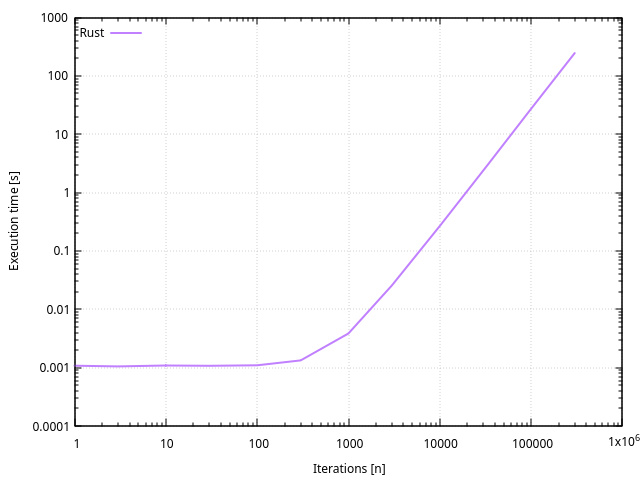
Fortran
Fortran est un langage assez ancien et démodé qui a très longtemps été utilisé pour des calculs et simulations techniques et scientifiques à partir de l’époque des ordinateurs mainframes à la fin des années 50.
Comme c’est un langage très ancien qui a évolué, j’ai décidé de choisir la version Fortran 90, qui permet l’écriture d’instructions en caractères minuscules et autorise une indentation simplifiée. Les versions plus récentes n’apportent pas d’instructions ni de principes qui sont utiles dans ce cas, mais permettent de compiler du code Fortran 90. On rencontre aussi le même cas qu’avec Python où le code n’est pas vectorisable, où on pourrait utiliser les célèbres bibliothèques LINPACK ou LAPACK14.
Performances
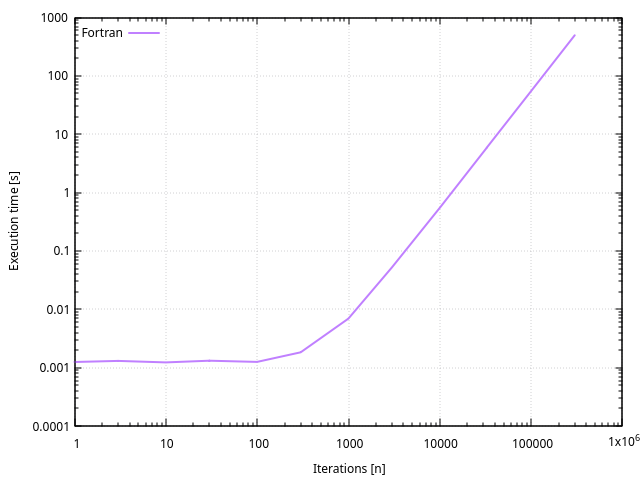
Ada
Ada est un autre langage assez ancien qui a longtemps été utilisé dans des environnements où la fiabilité est critique, dont l’aérospatiale. Il a la réputation d’être très le contraire de Python, où toute déclaration ou utilisation d’instructions ou de variables sont explicites.
Comme c’est un langage assez différent des autres, la durée d’écriture a été plus longue que pour les autres programmes151617.
Performances
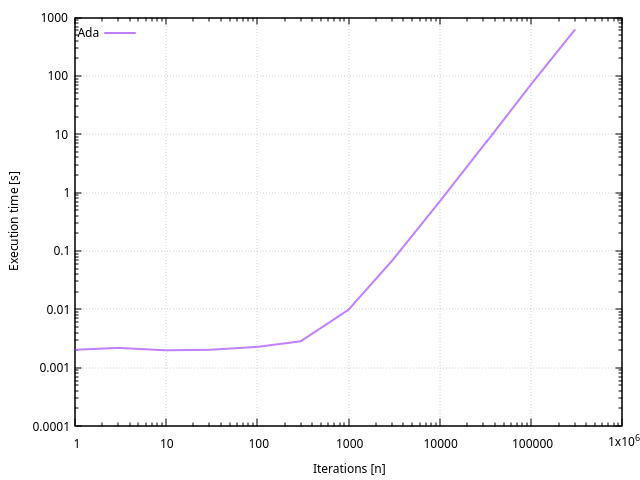
Comparaison
Conditions
Avant de comparer les performances, et pour que les mesures soient reproductibles, il faut comparer les conditions dans lesquelles les programmes ont été écrits, compilés, et exécutés.
Tous les programmes sont écrits avec l’éditeur de texte kwrite 22.12.3, avec la coloration syntaxique.
| Langage | Compilateur | Version de compilateur | Version de langage | Ligne de commande de compilation |
|---|---|---|---|---|
| C | GCC | 12.2.0-14+deb12u1 | C99, compatible C89 | gcc -Wall -Ofast |
| C++ | G++ | 12.2.0-14+deb12u1 | C++20 | g++ -Ofast -Wall -std=c++20 |
| C++ OpenMP | G++ | 12.2.0-14+deb12u1 | C++20 | g++ -fopenmp -Ofast -Wall -std=c++20 |
| Python | Python | 3.11.2 | Python 3 | python3 |
| Go | go | go1.19.8 | - | go build |
| Bash | Bash | 5.2.15(1)-release | - | bash |
| Rust | Cargo + rustc | 1.63.0 | - | cargo build --release |
| Fortran | GFortran | 12.2.0-14+deb12u1 | Fortran 90 | gfortran -Ofast |
| Ada | GNAT | 12.2.0 | Ada 95 | gnat make |
Tous les programmes ont été exécutés par la même machine Lenovo Thinkpad T470 avec la configurations suivante :
- CPU : Intel Core i5-6300U, 2.4GHz, 2C/4T
- RAM : 8GB DDR4 2.133GHz, single-channel
- OS : Linux 6.1.0-29-amd64
- Distribution : Devuan daedalus (Debian 12.11 Bookworm)
Justesse
Avant de comparer les durées d’exécutions, il est indispensable de comparer la justesse ou l’exactitude du calcul approché18. Comme les types de variables sont les mêmes et que l’algorithme est identique, le résultat doit-être identique.
On compare les approximations calculées à la valeur M_PI de math.h19, les valeurs M_PIf32 ou plus précises ne changent rien à notre approximation beaucoup moins précise.
L’allure générale de la courbe ne montre aucune surprise : les courbes se superposent exactement, et plus le nombre d’itérations augmente, plus l’approximation est exacte.
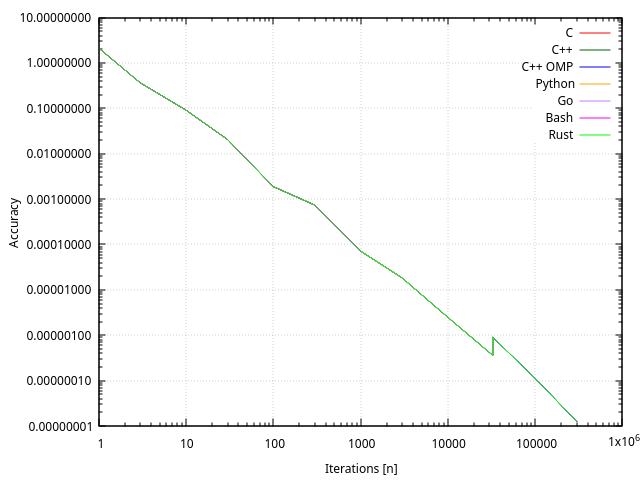
Plusieurs nombres d’itérations ont été testés : 1, 3, 10, 30, 100, 300, 1000, 3000, 10’000, 32’767, 32’768, 100’000, 300’000. Ces valeurs ont été choisies arbitrairement pour mesurer les performances, y compris les valeurs 32’767 et 32’768. Sauf qu’on remarque un comportement curieux à ce voisinage : la valeur de l’erreur double, et le comportement est reproductible avec tous les langages, peu importe le type de variables qu’ils utilisent.
Ce comportement semble surtout dépendre de la façon dont l’opération de division est effectuée : . Cette opération utilise des variables de type float642021, dont la justesse peut varier d’au moins un LSB22.
Balayer beaucoup plus d’itérations confirme ce comportement :
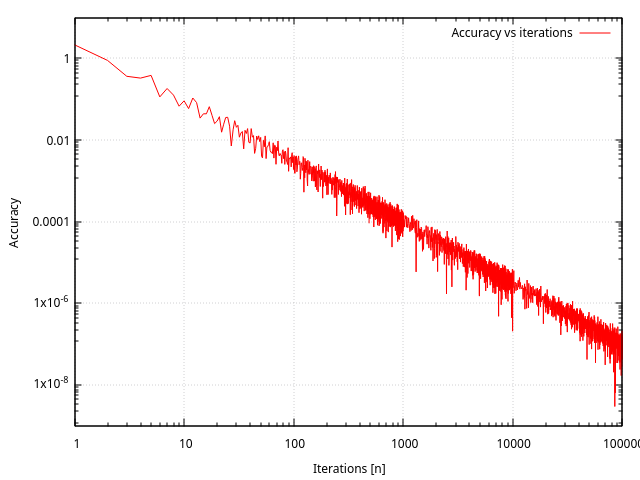
Performances
La comparaison de la durée d’exécution montre de grandes différences entre les langages interprétés et les langages compilés.
| Langage | C | C++ | C++ OpenMP | Python | Go | Bash | Rust | Fortran | Ada |
|---|---|---|---|---|---|---|---|---|---|
| Écriture [min] | 60 | 10 | 20 | 5 | 20 | 20 | 30 | 45 | 90 |
| Nombre de lignes | 45 | 27 | 50 | 17 | 30 | 24 | 27 | 26 | 35 |
| Compilation [ms] | 160 | 717 | 880 | - | 240 | - | 590 | 92 | 11 |
| Taille du fichier [kB] | 16 | 16 | 16 | - | 1’208 | - | 364 | 16 | 24 |
| Exécution n=100 [ms] | 1.2 | 1.8 | 2.1 | 215 | 1.7 | 1’840 | 1.1 | 1.4 | 2.3 |
| Exécution n=10’000 [ms] | 170 | 174 | 116 | 45’300 | 578 | 267 | 550 | 706 | |
| Exécution n=100’000 [s] | 38.6 | 38.8 | 17.9 | 57.1 | 27.3 | 54.5 | 71.7 |
La durée nécessaire à écrire le code en C n’est pas très juste, puisqu’il a fallu optimiser le code pour la vitesse d’exécution, et que ces optimisations ont ensuite servi aux programmes C++.
Améliorations possibles
- L’algorithme est volontairement simple, il en existe d’autres qui convergent plus rapidement23
- Approcher les portions de cercle avec un triangle plutôt qu’un carré converge plus rapidement en coûtant peu de calculs en plus
- Il est possible d’utiliser les invariances du disque pour n’en balayer qu’un quadrant et effectuer 4 fois moins de calculs
- Il est possible d’éviter des calculs en inscrivant un carré de côté dans le disque, et 4 carrés de côté aux coins
Code C amélioré
Invariances du disque
Un disque est invariant quand on lui applique une rotation à partir de son centre. Comme on utilise un repère orthonormal, on peut le séparer en 4, et donc calculer 4 fois plus rapidement.
for(i = 0; i <= n; i++) {
for(j = 1; j <= n; j++) {
if(i*i + j*j < n*n)
count++;
}
}
pi = 4.0 * (double) count/(n*n);Ici, on a remplacé i = -n et j = -n par i = 0 et j = 1, et multiplié count par 4, ce qui rend le calcul global 4 fois plus rapide.
Approximation par triangles
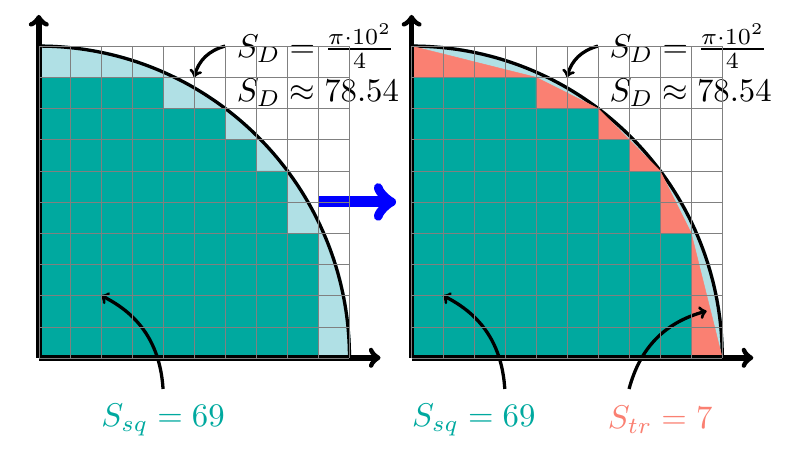
Dans notre cas, on découpe un disque en petits carrés dont on somme la surface. Leur surface est strictement inférieure à celle d’un disque, mais l’approche rapidement lorsque le nombre de carrés augmente.
for(i = 0; i <= n; i++) {
for(j = 1; j <= n; j++) {
if(i*i + j*j < n*n)
count++;
if(i*i + j*j == n*n)
hcount++;
}
}
count += hcount/2;
pi = 4.0 * (double) count/(n*n);On a rajouté la variable hcount pour compter les triangles aux limites du disque. La boucle est la partie la plus lente à effectuer, le test et l’incrémentation d’un compteur ajoutent peu de complexité.
C’est comparable à d’autres formules24 qui permettent d’approximer plus finement qu’un escalier, l’approximation est plus précise et converge plus rapidement.
Simplification
Qu’est-ce qui est plus rapide que de calculer ? Ne pas calculer.
On peut séparer le disque en plusieurs zones, avec une contrainte : .
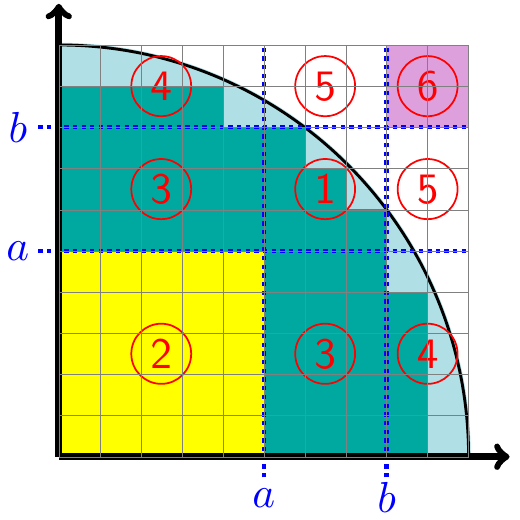
- Les zones , et sont symétriques, on peut donc ne calculer leurs valeurs qu’une seule fois, puis les multiplier par deux
- La zone est toujours à l’intérieur du disque, sa surface est obtenue par qui est un calcul simple et rapide
- La zone est toujours à l’extérieur du disque, sa surface est nulle, pas besoin de la calculer
- On ne peut pas éviter de calculer les valeurs des zones et qui peuvent-être à la frontière du disque, en fonction des valeurs et choisies
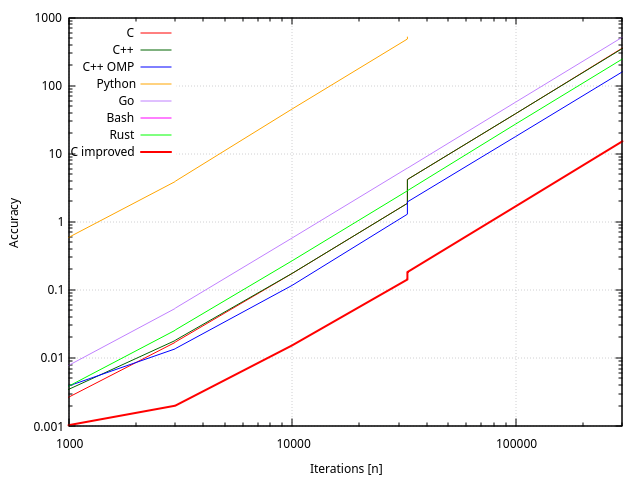
Performances
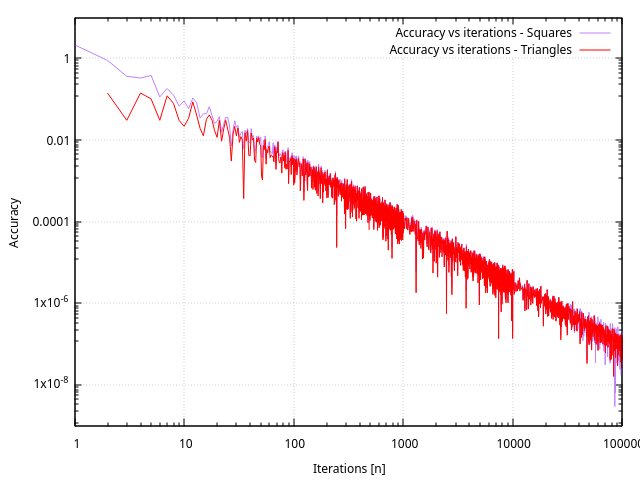
La convergence est plus rapide pour de faibles nombres d’itérations, mais elle n’est pas extrêmement visible avec des nombres d’itérations élevés.
| Langage | C | C optimisé |
|---|---|---|
| Écriture [min] | 60 | 120 |
| Nombre de lignes | 45 | 103 |
| Compilation [ms] | 160 | 169 |
| Taille du fichier [kb] | 20 | 20 |
| Exécution n=100 [ms] | 1.2 | 0.8 |
| Exécution n=10’000 [ms] | 170 | 15.3 |
| Exécution n=100’000 [s] | 38.6 | 1.67 |
Le programme s’exécute 1.5 à 23 fois plus vite que la première version en langage C.
Le code source est disponible25 sous license CC BY-NC.
Références
Les types automatiques existent depuis la norme C23.↩︎
Ada95 Language Reference Manual (LRM) ISO/IEC 8652:1995 - Ada resource Association↩︎
File:Accuracy (trueness and precision).svg - Wikimedia Commons↩︎
File:Accuracy (trueness and precision).svg - Wikimedia Commons↩︎
Page maison de Simon Plouffe Home Page, Pi Formulas, Algorithms and Computations - Fabrice Bellard↩︎
Taylor series - Wikipedia Lagrange polynomial - Wikipedia, Pi - Archimedes - Nick Craig-Wood, entre autres↩︎
- ← Previous page
Comparaison de langages de programmation (4) : Génération d'images - Next page →
Disjoncteur Magnéto-Thermique
Electronics Électronique puissance semiconducteur semiconductors power Hardware CPE INSA Xavier Bourgeois
 RSS - Blog
RSS - Blog